1 年前发表21 天前更新 xeonds 42 分钟读完 (大约6248个字)52次访问

计算机视觉学习笔记

之前导论课程上学的基本都是思想和原理，到这里就开始接触真正数学和工程的方法了。

序

这门课的研究思路很清晰，就是围绕标题，自底向上，借助数学工具，一步一步实现各种复杂的功能以及算法，最终一步步接近让计算机拥有“视觉”的目标。

首先是数据的表示，概念的抽象，如何用离散的数据去近似抽象的视觉这个概念。这个过程通过直观理解和数学工具，以及建模方法，为计算机视觉提供了一种可行的数学上的表示和运算方法：像素，以及基于像素的一系列运算，比如滤波，仿射变换，更高自由度的变换，基于像素颜色值的变换等等，以及由这一系列变换得到的图像特征。

其次，是研究在图像的像素模型下，利用数学方法去研究分析以及利用图像特征的方法。这其中，就有诸如角点检测，边缘检测，全景图拼接以及处理等命题。

生成对抗网络GAN

通俗来说就是让两个网络作为对抗组，比如说生成图片的NN和鉴别图片的NN，两方轮流作为输入输出（也就是交替训练），在循环中不断提升两个网络的效果，最终达到生成内容以假乱真的效果。NN炼丹的关键是其中的loss函数设计，不过他们的做法是直接用另一个NN作为这个NN的loss函数来回馈训练效果。

目前比较突出的成果一个就是近几年的Stable Diffusion，算是这里边比较突出的一个了。这东西在图像的有损压缩里边用的也多，至于有损压缩的应用嘛，一般在一些需要使用算力去换带宽的场合很适用，比如卫星数据传输。其他应用就是图像的填充和补全，比如合理推测图像的缺失部分内容。另外就是，网络的输入不一定是噪声，输出也不一定是真假。改变其输入和输出的类型，可以赋予NN以不少是实用场景。

GAN的优点是效果好，比以前用的高斯模糊的效果都很好。但是问题也很突出，就是GAN很难训练。GAN的两方是生成器和判别器，训练的结果很大程度上与两方的能力是否足够接近有很大关系。

另外就是GAN的思想重点在对抗，并没有要求其他的条件。所以比如说可以有多个判别方，有多个生成方等。

Attention Is All You Need

注意力机制一开始是应用于机器翻译领域，通过一个合适的重点词语权重标注机制，让算法更有重点地提取概要。如今的GPT也很大程度上受到注意力机制的启发才产生了不断预测下一个词向量概率的朴素思想。

注意力机制可以理解成给分词加上权重。将一个句子进行分词作为一个向量，将这个词语向量通过Softmax这样的激活函数进行处理之后，再借助矩阵进行变换，从而得到处理后的，带有权重的词向量。处理后的词向量，权重总和为1。加权后的句子，再进行翻译，效果就会好很多了。

至于将Attention思想迁移到CV领域进行应用的方法，关键是将图像”语义化“。一个常用的方法是将图像分割，分割成小块，对每个小块采用相同的思想。这就是VIT（Vision Transformer）的思想。

激活函数

Softmax

Softmax函数是一种常用的激活函数,主要用于将多分类问题中的输出值转换为概率分布。在神经网络中,输出层通常使用softmax函数,将输出值转换为每个类别概率。

Softmax函数的定义如下:
$Softmax(x) = e^(x_i) / (e^(x_1) + e^(x_2) + … + e^(x_n))$
其中,x是一个K维向量,Softmax函数的输出也是一个K维向量,并且每个元素的范围都在0到1之间,并且所有元素的和为1。

在多分类问题中,假设输出层有K个神经元,每个神经元代表一个类别。Softmax函数的作用是将输出层的输出转换为每个类别对应的概率。例如,如果输出层输出为[1.2, 2.3, 3.1],则对应的概率为[0.21, 0.34, 0.45]。

Softmax函数可以解决输出值非常大的问题,因为它可以防止输出值过大而导致的梯度消失或梯度爆炸。此外,Softmax函数还可以进行归一化,使得概率和为1,使得概率分布更加合理。

期末划重点咯

sudo 老师给我分

有个压缩包，里边画红钩的都是重点

占比大概NN和传统方法4-6开

Chap 1 没啥重点
- 什么是光，可见光谱的范围这些的
- 人的视觉系统这些概念啥的
- 三色光的相关内容
Chap 3 重点
- 灰度图（取值范围），RGB
- 图像两种基本运算
- 矩阵的运算
- 滤波概念，高斯滤波
- 卷积，点乘积，性质，计算过程strike, padding计算结果图像尺寸这些的
Chap 4 边缘检测
- 边缘定义,为啥是边缘
- 图像的梯度
- 噪声
- 边缘检测器：sobel算子,roberts算子,prewwit算子等
- 边缘存在的问题：噪声，拟合等
Chap 6 图像插值
- 线性插值，上下采样等，高斯金字塔
- 图像放大的插值算法（超分）
  - 最近邻，双线性，三次插值。不过现在都用GNN做超分了
Chap ? 特征匹配
- 典型特征匹配计算方法
- 特征和特真不变性：啥特征的啥不变性 SIFT特征
Chap 7 图像变换
- 几种变换方式
- 线性变换：变灰度，变尺度等
- 按照变换剧烈程度递增：平移，旋转，仿射，投影
- 得记得变换矩阵的特征,大概得看明白
Chap 8 图像配准没啥讲的
Chap 11 单视图建模
- 消失线和消失点等得会计算
- 双试图立体视觉：视差和深度计算
- 窗口配准
- 极点极线极面
- 本质矩阵，基本矩阵是谁到谁的映射
- 深度估计
Chap 14 图像三维重建
- 一个相机转着拍内参矩阵不变，为了配窗
- 重复的问题
Chap 16 机器视觉
- 激活函数和矩阵计算
- 神经网络结构
- 卷积网络的池化操作
- 反向传播：对w求导而非对x求导，而且得会算反向传播函数
Chap 18 图像分割
- 语义分割和实例分割
- 分割手段：边缘检测,聚类等方法
Chap 19 目标检测与分类
- 输出：中心型，边界型
- 两个方法：两步法，一步法（Yolo）
Chap 21 实操
- 玩玩pytorch
Chap 23 神经网络前沿
- GAN
- Attention(q,k,v)
  - Softmax

计算机视觉复习

找到一个学长的复习笔记如下

图像和图像滤波

什么是滤波

形成一个新的图像，其像素是原始像素的组合
什么时候利用滤波
- ==增强图像：== 降噪、锐化
- ==提取信息：== 提取边缘或轮廓

滤波的种类：

线性滤波：用相邻的线性组合（加权和）替换每个像素
- 线性组合的系数称为权重核
卷积：(权重核反转（水平和垂直）)
$G [ i , j ] = \sum _ { u = - k } ^ { k } \sum _ { v = - k } ^ { k } H [ u , v ] F [ i - u , j - v ]$
记为
$G=H*F$
相关：
$G [ i , j ] = \sum _ { u = - k } ^ { k } \sum _ { v = - k } ^ { k } H [ u , v ] F [ i + u , j + v ]$
记为：
$G = H \otimes F$
高斯滤波

==从图像中删除「高频」分量（低通滤波器）==

==高斯核函数==：
$G _ { \sigma } = \frac { 1 } { 2 \pi \sigma ^ { 2 } } e ^ { - \frac { \left( x ^ { 2 } + y ^ { 2 } \right) } { 2 \sigma ^ { 2 } } }$

滤波的应用

锐化滤波器：
$F + \alpha (F-F*H)$
阈值滤波器
$g ( m , n ) = \left{ \begin{array} { c c } { 255 , } & { f ( m , n ) > A } \ { 0 } & { \text { otherwise } } \end{array} \right.$
==阈值滤波器不是线性滤波==
相关和卷积的定义和关系
高斯核
- 调节哪个参数
什么是线性滤波器
去燥使用什么滤波

边缘检测

边缘的特征

怎样通过导数来反映边缘

==对于图像强度的一阶导数，边缘对应于导数的极值==

如何计算数字图像的导数？

重建连续图像，然后计算导数
采用离散导数（有限差分）: ==图像的梯度相当于两个相邻像素之间的差值==
$\frac { \partial f } { \partial x } [ x , y ] \approx F [ x + 1 , y ] - F [ x , y ]$
可以使用线性滤波器实现

==梯度的方向 垂直于边缘的方向==，梯度的方向是图像函数 f(x,y) 变化最快的方向，当图像中存在边缘时，一定有较大的梯度

图像梯度

图像梯度是图像函数在 x ,y 两个方向的导数，

幅值:
$| \nabla f | = \sqrt { \left( \frac { \partial f } { \partial x } \right) ^ { 2 } + \left( \frac { \partial f } { \partial y } \right) ^ { 2 } }$
方向：
$\theta = \tan ^ { - 1 } \left( \frac { \partial f } { \partial y } / \frac { \partial f } { \partial x } \right)$
==要计算图像梯度，首先要图像去噪，使用高斯核在图像上卷积，平滑图像==

可以将两次滤波（高斯滤波、差分滤波）合成一步实现

mark

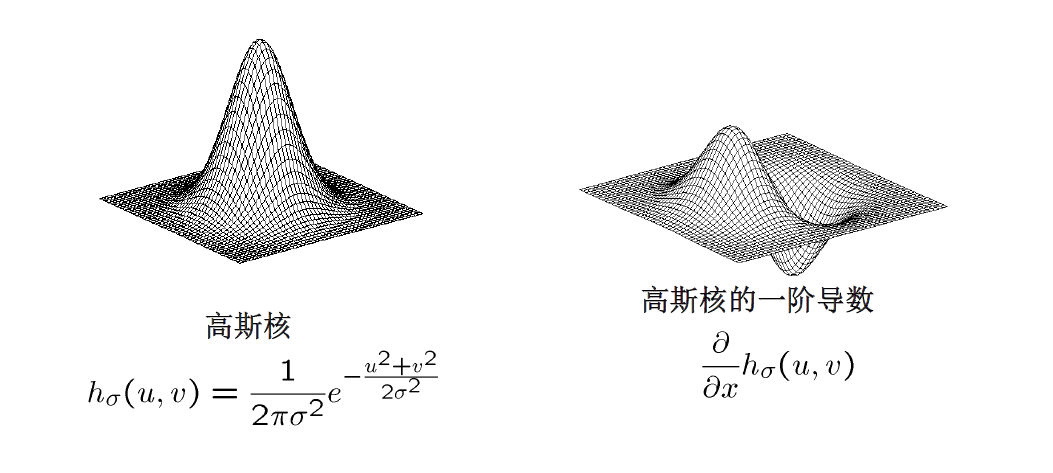
二维边缘检测使用的图像算子：

Sobel 算子

mark

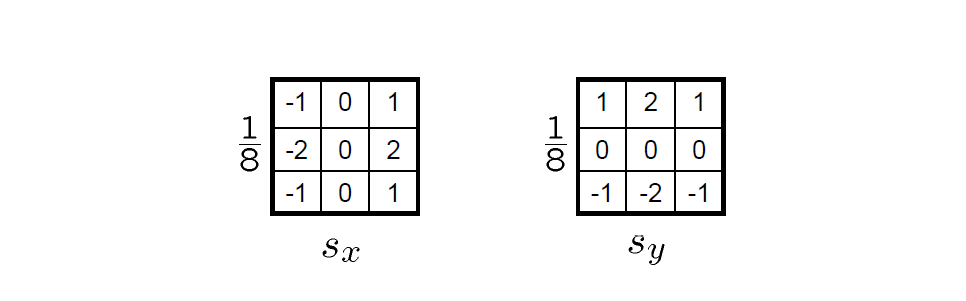
非最大抑制

检查像素是否为沿梯度方向的局部最大值 （需要进行像素差值？）

==Canny 边缘检测器==
1. 用高斯导数滤波
2. 获得梯度的幅值和方向
3. 非最大抑制
4. 连接与滞后阈值化：
  - 定义高低两个阈值
  - 用==高阈值来寻找边缘曲线的起点，用低阈值来确定后继点==，进行连接
Canny 边缘检测器的参数：
- $\sigma:$ 高斯模糊的宽度：大的 $\sigma$ 可以检测大尺度边缘， $\sigma$ ==越小，能检测到的细微边缘就越多==
- 高阈值
- 低阈值

图像的导数
图像的梯度是什么（两个方向的导数）（复制和方向）
去噪
二维边缘检测
- 列举几个图像算子
费最大值抑制
边缘检测器

图像的插值和重采样

图像采样

采样率

==奈奎斯特采样率： 采样率 >= 2*图像中的最大频率==

若原始图像的频率过高，先对图像滤波，然后子采样，构建高斯金字塔

图像插值

最近邻差值：重复 n 次
双线性插值：利用输入图像中与输出图像像素点映射位置最邻近的4个像素点的颜色值(或灰度值)计算输出图像中像素点的颜色值(或灰度值)
双三次插值：为了得到更精确的(x’,y’)的颜色值(或灰度值)g(x’,y’),就不仅需要考虑与(x’,y’)点最邻近的四个点对它的影响,还要考虑到该点周围16个相邻点的颜色值(或灰度值)对它的影响。

角点检测

Harris 角点检测：将窗口平移，比较平移前后 w 内每个像素的差异平方和（SSD）
$E ( u , v ) = \sum _ { ( x , y ) \in W } [ I ( x + u , y + v ) - I ( x , y ) ] ^ { 2 }$

$\begin{aligned} E ( u , v ) = & \sum _ { ( x , y ) \in W } [ I ( x + u , y + v ) - I ( x , y ) ] ^ { 2 } \ \approx & \sum _ { ( x , y ) \in W } \left[ I ( x , y ) + I _ { x } u + I _ { y } v - I ( x , y ) \right] ^ { 2 } \ \approx & \sum _ { ( x , y ) \in W } \left[ I _ { x } u + I _ { y } v \right] ^ { 2 }\ \approx Au^2+2Buv +Cv^2\ \end{aligned}$

$A = \sum _ { ( x , y ) \in W } I _ { x } ^ { 2 } \quad B = \sum _ { ( x , y ) \in W } I _ { x } I _ { y } \quad C = \sum _ { ( x , y ) \in W } I _ { y } ^ { 2 }$

算法实现：

计算图像在 X， Y 两个方向的梯度
计算两个方向上梯度的乘积
使用高斯函数对 $I_x^2,I_y^2,I_xI_y$ 进行高斯加权，生成矩阵的元素 A，B，C
计算每个像素的 Harris 响应值 R，并对小于某个阈值的 R 置 0
$R = \left{ R : \operatorname { det } M - \alpha ( \operatorname { trace } M ) ^ { 2 } < t \right}$
在邻域内进行非最大抑制，局部最大值即为图像的角点

特征不变性

我们希望角点的位置对光度变换具有不变性（图像变换之后，角点位置不变），对几何变换具有协变性（相应位置检测到同一特征）

不变性：

对平移、旋转协变
对强度平移具有不变性，对强度缩放不具有不变性
对缩放不具有不变性
- 需要同时在位置和尺度上查找：自动尺度选择

自动尺度选择：

在高斯金字塔中使用固定大小的窗口，寻找具有局部最大值的尺度

斑点检测：

斑点是指二维图像中和周围颜色有颜色差异和灰度差异的区域,因为斑点代表的是一个区域,所以其相对于单纯的角点,具有更好的稳定性和更好的抗干扰能力.

核函数：
- 高斯拉普拉斯：
  $\nabla ^ { 2 } g = \frac { \partial ^ { 2 } g } { \partial x ^ { 2 } } + \frac { \partial ^ { 2 } g } { \partial y ^ { 2 } }$
- 高斯差分函数
  $D o G = G ( x , y , k \sigma ) - G ( x , y , \sigma )$
当 $\sigma = r/\sqrt{2}$ 时，响应最大，图像黑白反向时，响应最小，因此将高斯拉普拉斯算子响应达到峰值的 $\sigma$ 值，称为特征尺度
怎么实现特征的不变
Harris 检测的步骤

特征描述与匹配

特征描述符

MOPS:
1. 选取特征点周围 40*40 的方形窗口
2. 缩放到 1/5 大小
3. 旋转特征向量方向到水平
4. 在以特征为中心的 8*8 方形窗口内采样
5. 规格化（强度减去平均值，除以标准差，均值为0，方差为1）
SIFT：尺度不变特征转换

mark
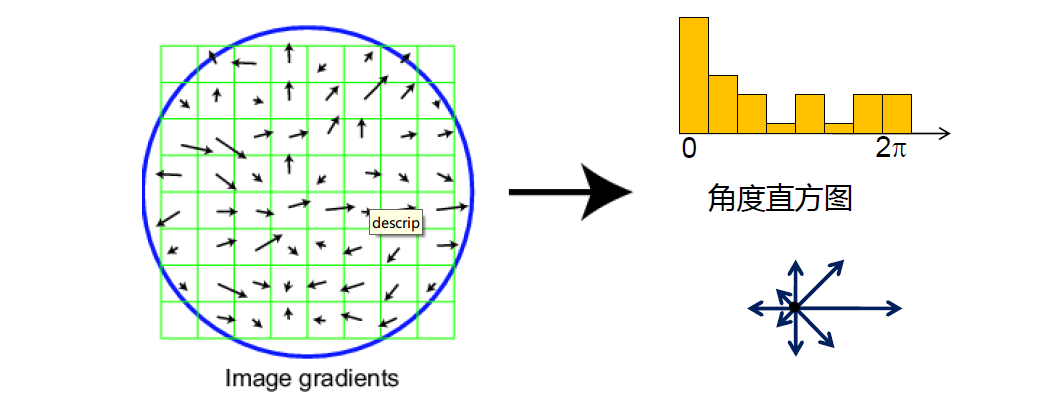
1. 在所检测的特征周围取 16*16 的窗口
2. 为每个像素计算边缘方向
3. 去除弱的边缘方向（设定阈值）
4. 为剩余边缘方向建立直方图

特征匹配

特征距离
- 更好的方法：距离比
  
  $f_2$ 是 $f_1$ 在 $I_2$ 中最好的 SSD 匹配， $f_2^\prime$ 次之
  $距离比 = \frac{||f_1-f_2||}{||f_1-f_2^\prime||}$
测量特征匹配的性能
- 真正例率（TPR）（召回率） = 匹配到的真正例数 / 所有真正例数
- 假正例率（FPR） = 匹配到的假正例数/所有真正例数
- ROC 曲线：以 FPR 为横轴，TPR 为纵轴
- AUC：曲线下的面积，越大越好

变换与卷绕

什么是图像卷绕：更改图像的定义域

常见的变换

平移
欧式变换：平移+旋转
相似变换：平移+旋转+等比放缩
仿射变换：平移+旋转+等比放缩+剪切
投影变换：原来平行的线不再平行，但还是保持直线性

线性变换

等比缩放：比例S
旋转角度
剪切
镜像

线性变换的性质

原点到原点

直线到直线

平行线保持平行

比率被保持

线性变换的组合是线性变换

平移不是 2D 坐标上的线性变换，我们需要 添加一个坐标 -> 齐次坐标

仿射变换

任何最后一行为 [0,0,1] 的 3·3 矩阵表示的转换称为仿射变换，仿射变换是线性变换和平移的组合

变换完成后，平面位置不变

基本的仿射变换：

平移、缩放、2D 平面旋转、剪切

mark
仿射变换是线性变换 + 平移

性质

原点不一定到原点
直线到直线
平行还平行
保持比率
闭包

透视变换、投影变换、同态映射

最后一元素固定为1 ，共有8个参数， 是成像平面的变换，仿射变换是特例

原点不一定映射到原点
平行线不一定保持平行
不保持比率
闭包

卷绕

卷绕有两种：

前向卷绕
反向卷绕

变换后的像素位置如果不是整数： 将像素值分配给四个最近邻，记录每个点的权重并在最后归一化

效果：混叠与模糊

反向卷绕

先获取每个像素在原图像中对应的位置处的像素值（逆变换）

如果像素位置不是整数，利用原来相邻像素值插值
- 可能的插值滤波器
  - 最近邻
  - 双线性
  - 双三次
  - 窗 sinc
- 需要防止锯齿和混叠（需要预先滤波）
变换有哪几种
卷绕有两种

卷绕之后产生了非整数值怎么办
常见的变换
- 旋转
- 平移
- 基本仿射变换
- 仿射变换的含义是什么

图像配准

配准算法的流程，怎么实现

特征提取
匹配
反向变换
插值

优化方式

最小二乘法

图像配准算法

给定图像 A 和 B

计算 A、B 的图像特征
匹配 A、B 之间的特征
使用匹配集计算 A 到 B 的单应映射矩阵的最小二乘解

最小化残差平方和

定义残差：
$\begin{array} { l } { r _ { \mathbf { x } _ { i } } \left( \mathbf { x } _ { t } \right) = \left( \mathbf { x } _ { i } + \mathbf { x } _ { t } \right) - \mathbf { x } _ { i } ^ { \prime } } \ { r _ { \mathbf { y } _ { i } } \left( \mathbf { y } _ { t } \right) = \left( \mathbf { y } _ { i } + \mathbf { y } _ { t } \right) - \mathbf { y } _ { i } ^ { \prime } } \end{array}$
将 n 个点形成的 2n 个方程写成矩阵方程：
$\left[ \begin{array} { l l } { 1 } & { 0 } \ { 0 } & { 1 } \ { 1 } & { 0 } \ { 0 } & { 1 } \ { 0 } & { 1 } \ { \vdots } \ { 1 } & { 0 } \ { 0 } & { 1 } \end{array} \right] \left[ \begin{array} { l } { x _ { t } } \ { y _ { t } } \end{array} \right] = \left[ \begin{array} { c } { x _ { 1 } ^ { \prime } - x _ { 1 } } \ { y _ { 1 } ^ { \prime } - y _ { 1 } } \ { x _ { 1 } ^ { \prime } - x _ { 2 } } \ { y _ { 2 } ^ { \prime } - y _ { 2 } } \ { \vdots } \ { x _ { n } ^ { \prime } - x _ { n } } \ { y _ { n } ^ { \prime } - y _ { n } } \end{array} \right]$

$At =b$

找到 t ，最大限度的减少
$| \mathbf { A } \mathbf { t } - \mathbf { b } | ^ { 2 }$

$\begin{array} { c } { \mathbf { A } ^ { \mathrm { T } } \mathbf { A } \mathbf { t } = \mathbf { A } ^ { \mathrm { T } } \mathbf { b } } \ { \mathbf { t } = \left( \mathbf { A } ^ { \mathrm { T } } \mathbf { A } \right) ^ { - 1 } \mathbf { A } ^ { \mathrm { T } } \mathbf { b } } \end{array}$

对于仿射变换：
$\left[ \begin{array} { l } { x ^ { \prime } } \ { y ^ { \prime } } \ { 1 } \end{array} \right] = \left[ \begin{array} { l l l } { a } & { b } & { c } \ { d } & { e } & { f } \ { 0 } & { 0 } & { 1 } \end{array} \right] \left[ \begin{array} { l } { x } \ { y } \ { 1 } \end{array} \right]$
有六个未知数，每个匹配有两个方程，我们需要三个匹配

残差：
$\begin{aligned} r _ { x _ { i } } ( a , b , c , d , e , f ) & = \left( a x _ { i } + b y _ { i } + c \right) - x _ { i } ^ { \prime } \ r _ { y _ { i } } ( a , b , c , d , e , f ) & = \left( d x _ { i } + e y _ { i } + f \right) - y _ { i } ^ { \prime } \end{aligned}$
对于同态映射（透视变换）
$\left[ \begin{array} { c } { x _ { i } ^ { \prime } } \ { y _ { i } ^ { \prime } } \ { 1 } \end{array} \right] \cong \left[ \begin{array} { l l l } { h _ { 00 } } & { h _ { 01 } } & { h _ { 02 } } \ { h _ { 10 } } & { h _ { 11 } } & { h _ { 12 } } \ { h _ { 20 } } & { h _ { 21 } } & { h _ { 22 } } \end{array} \right] \left[ \begin{array} { c } { x _ { i } } \ { y _ { i } } \ { 1 } \end{array} \right]$

$\begin{aligned} x _ { i } ^ { \prime } \left( h _ { 20 } x _ { i } + h _ { 21 } y _ { i } + h _ { 22 } \right) & = h _ { 00 } x _ { i } + h _ { 01 } y _ { i } + h _ { 02 } \ y _ { i } ^ { \prime } \left( h _ { 20 } x _ { i } + h _ { 21 } y _ { i } + h _ { 22 } \right) & = h _ { 10 } x _ { i } + h _ { 11 } y _ { i } + h _ { 12 } \end{aligned}$

mark

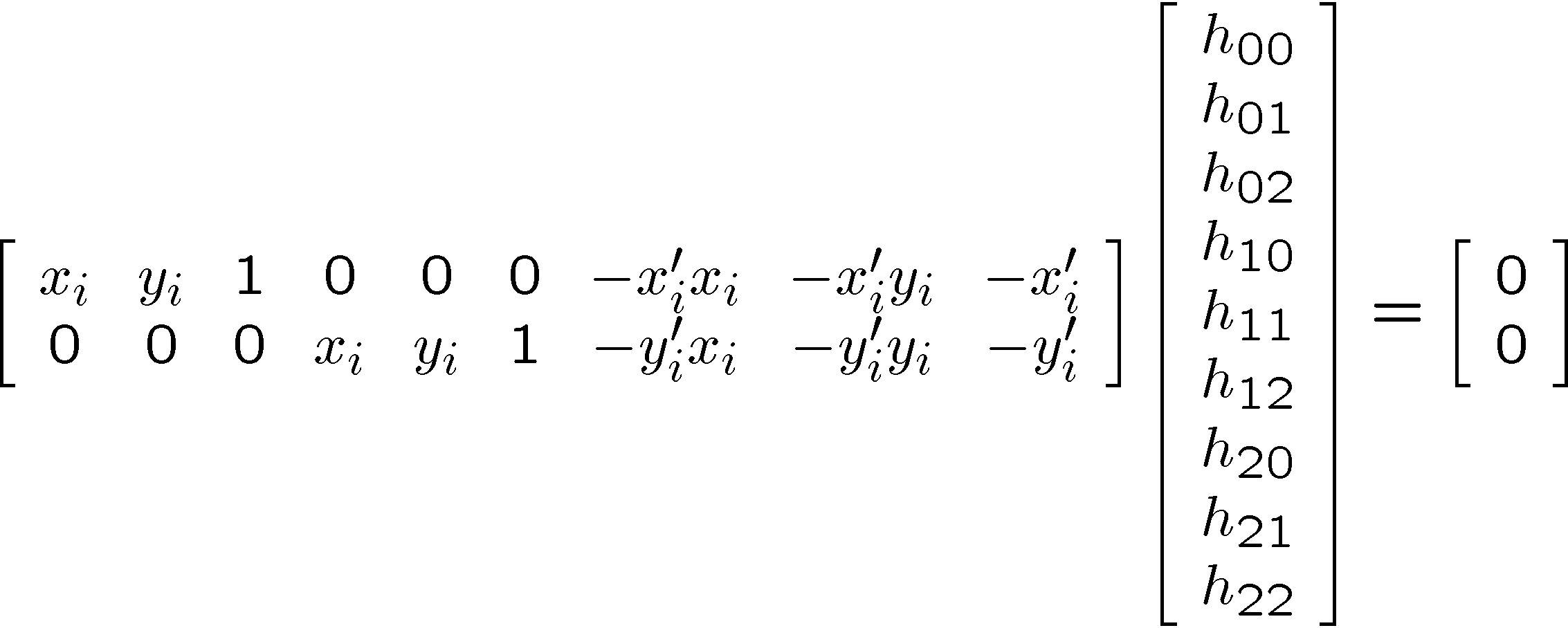
Ah = 0 的非平凡最小二乘解，即为 $A^TA$ 具有最小特征值的特征向量

RANSAC 随机抽样一致

如何计算

随机抽取
计算匹配误差

Ransac 算法

随机选择 S 个样本
- 通常 s 等于可以求解模型的最少样本数量
使用这 s 个样本求得一个解
计数符合模型的 inliers 数
重复 N 次
选择具有最多 inliers 数的模型
使用所有的 inliers 点，采用最小平方拟合

实验轮数的确定

$p$ 数内点的概率
$s$ 是每次实验使用样本点的数目
$P$ 为实验最终成功找到正确解的概率
$R$ 为实验轮数

$$
\begin{array} { l }

计算机视觉学习笔记

https://mxts.jiujiuer.xyz/2023/11/06/计算机科学/计算机视觉/计算机视觉学习笔记/

作者

xeonds

发布于

2023-11-06

更新于

2025-03-15

许可协议

#Python 计算机视觉

计算机视觉学习笔记

序

生成对抗网络GAN

Attention Is All You Need

激活函数

Softmax

期末划重点咯

计算机视觉复习

图像和图像滤波

边缘检测

边缘的特征

图像梯度

二维边缘检测使用的图像算子：

非最大抑制

图像的插值和重采样

图像采样

图像插值

角点检测

特征不变性

特征描述与匹配

特征描述符

特征匹配

变换与卷绕

线性变换

仿射变换

透视变换、投影变换、同态映射

卷绕

图像配准

图像配准算法

最小化残差平方和

RANSAC 随机抽样一致

Ransac 算法

实验轮数的确定

作者

发布于

更新于

许可协议

评论

目录

链接

最新文章

归档

最新文章

归档