第一章:概率论的基本概念
概率论的内容组织线索:
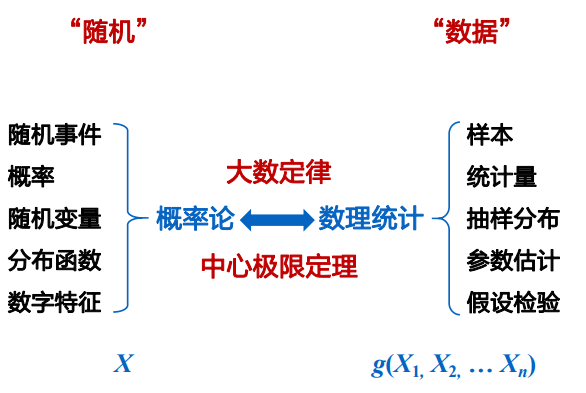
随机现象与随机实验
随机现象分为确定性现象、不确定性现象。前者结果确定,例如太阳东升西落;后者现象不确定,例如未来的天气。随机试验E表示,针对随机现象的观察、记录、试验。它有如下特点:
- 可重复
- 全部可能性已知
- 试验前不确定试验结果
样本空间与随机事件
样本空间$\Omega$ 指的是随机试验E的所有结果构成的集合,记为$\Omega={e}$。每个结果$e$是$\Omega$中一个元素,称为样本点。其中的元素数量可以无限。
一些随机试验E的样本点的集合(可空)称为随机事件,也称事件。全体样本点构成的集合称为样本空间,记为$\Omega$。每次试验,当且仅当该子集的一个样本点出现时,称这一事件发生。
如果Ω只包含有限个样本点,则单个样本点构成的事件(单点集),称为基本事件。
如果将Ω亦视作事件,是自身子集,则每次试验,Ω总是发生,称为必然事件。
空集Φ也是样本空间Ω的子集,不包含任何样本点,称为不可能事件。
事件间的关系
事件间有如下几种运算:
- 包含
- 并事件(至少一个发生)
- 交事件(同时发生),简写为AB
- 差事件:一个发生且另一个不发生
对应几种运算律:
- 交换律:并事件/交事件顺序可互换
- 结合律:A ∪ (B ∪ C) = (A ∪ B) ∪ C,A ∩ (B ∩ C) = (A ∩ B) ∩ C
- 分配律:
$$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$$
$$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$$ - 德摩根律:
$$\overline{A\cup B}=\overline{A}\cap \overline{B}=\overline{A}\overline{B}$$
$$\overline{A\cap B}=\overline{A}\cup \overline{B}$$
也有几种关系:
- 互斥:A、B不同时发生
- 对立/互逆:每次试验A、B必有一个发生。A的逆事件记作$\overline{A}$。
概率及其性质
在相同的条件下,进行了n次试验,其中事件A发生的次数$n_A$称为事件A发生的频数,比值$n_A/n$称为事件$A$发生的频率 , 记为$f_n(A)$。其中,频率取值范围$[0,1]$,且$f_n(\Omega)=1$。对于一组互不相容的事件而言,其并事件的频率为各自频率之和。
重复试验的次数n 逐渐增大时,频率 $f_n(A)$ 呈现稳定性,趋于某个常数$p$,这是统计的规律性。
由大数定律可证明,由频率的稳定性和频率的性质,得概率定义:重复试验的次数趋于无穷,频率$f_n(A)$接近概率$P(A)$。它有这么几个性质:频率取值范围$P(A)\geq 0$,且$P(\Omega)=1$。对于一组互不相容的事件而言,其并事件的概率为各自概率之和。这三性质就是柯尔莫哥洛夫公理。
它有如下性质:
- $P(\Phi)=0$
- 互不相容和事件的概率为每个事件的概率之和
- 若有$A\subset B$,则$P(B – A) = P(B) - P(A)$
- 对任一事件$A$, $P(A)\leq 1$
- 对立(互逆)事件的概率之和为1
- $P(A \cup B) = P(A) + P(B) - P(AB)$
上面这条,推广到任意多事件(或者直接整体法然后分n次使用上面这条),可得到:
$$
P(A_1\cup A_2\cup \cdots \cup A_n)=\Sigma_{i=1}^n P(A_i)-\Sigma_{1\leq i\leq j\leq n} P(A_iA_j)+ \Sigma_{1\leq i\leq j\leq k\leq n}P(A_iA_jA_k) + \cdots +(-1)^{n-1}P(A_1A_2\cdots A_n)
$$ - 极限性:设$A_1\subset A_2\subset \cdots \subset A_n\subset \cdots$是一系列上升的事件,则$\lim_{n\to \infty}P(A_n)=P(\cup_{i=1}^\infty A_i)$,反之也成立,将并换做交即可。

古典概率
古典概型(等可能概型) 的定义为:若试验 E 满足:
- 样本空间Ω包含有限个元素
- 出现每一样本点的概率相等 (等可能性),即试验中每个基本事件发生的可能性相同,故
$$
P(A)=\Sigma_{i=1}^kP({e_i})=\frac{k}{n}
$$
古典概型的样本空间由n个独立等可能事件组成,故每个基本事件的概率都为$\frac{1}{n}$。
排列和组合也是古典概率中重要的两个公式。排列表示从n个对象中按顺序选出m个对象:
$$
A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!}
$$
组合表示从n个对象中任选m个对象:
$$
C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}
$$
上面两式中,均有$n\geq m$。
加法原理和乘法原理高中就讲过,前者表示若完成一件事可有n类办法,其中,在第一类办法中有$m_1$种不同的方法,在第二类办法中有$m_2$种不同的方法,……, 在第n类办法中有$m_n$种不同的方法,则共有$\Sigma_{i=1}^nm_i$种方法完成这件事;而乘法原理表示若完成一件事需分解成n个步骤,其中,做第一步有 $m_1$种不同的方法,做第二步有$m_2$种不同的方法,……, 做第n步有$m_n$种不同的方法,则完成这件事的方法共有$\Pi_{i=1}^nm_i$种。
大学中新增加了实际推断原理,它的内容为:概率很小的事件在一次试验中几乎是不发生的。这符合我们对概率的直觉感受。注意这不能理解成“小概率事件从不发生”。与此同时,它还有另一层含义:小概率事件在大量重复试验中必然发生。
几何概率
在几何概型中,试验 E 满足:
- 所有可能的样本点构成的样本空间是“连续”的,构成了一个不可数无穷集
- 样本点是“均等的” ,即一次试验中,没有哪一个或哪一些比另一个或另一些更容易出现
直观上,每个事件发生的概率只与该事件的度量(如长度、面积、体积等)成正比例。
这种概率的计算公式为:
$$
P(A)=\frac{A_{len/size/volume}}{\Omega_{len/size/volume}}
$$
条件概率与概率的三大公式
这是第一章的重点内容。
条件概率的公式如下。意思为:A发生的条件下B发生的概率,等于AB同时发生的概率除以A发生的概率。设试验共包含n个基本事件,A有m(m>0)个,AB有k个,则
$$
P(B|A)=\frac{k}{m}=\frac{k/n}{m/n}\frac{P(AB)}{P(A)}
$$
条件概率 P(·/A) 具有概率的所有性质:非负性、规范性、可列可加性。它也满足其他性质,例如:

乘法公式
条件概率公式也可以反过来用来计算交事件的概率:$P(AB)=P(A)P(B|A)$,即乘法公式。
它也可以推广,逐项展开即可:

全概率公式
$$
P(B)=\sum_{i=1}^{n}P(A_i)P(B|A_i)
$$
上面的公式就是全概率公式。它表示$B$的概率可以用一系列概率和表示。
![[Pasted image 20230204114959.png]]
如上图所示,完备事件组是全样本空间的一个划分${A_i}$,$B$是一个横跨数个划分块的事件。造成B的可能有很多种,而全概率公式就是把这所有的概率加起来计算事件的总概率。
贝叶斯公式
$$
P(A_i|B)=\frac{P(A_iB)}{P(B)}=\frac{P(A_i)P(B|A_i)}{\sum{P(A_i)P(B|A_i)}}
$$
,且其中$P(B)\gt 0$。
继续按照上图的划分理解,这公式表示计算某因素$A_i$导致$B$发生的概率。
上面俩公式的用法是:明确起点事件、终点事件,画出起点到终点的所有路径。随后计算各路径的概率和(全概率)或者某路径在所有路径的占比(贝叶斯公式)。
独立性
后边再说