第二章:电阻电路分析
KCL/KVL独立方程
KCL独立方程

对于n个结点的连通图,有且仅有n-1个独立方程。
任取n-1个结点写出的KCL方程相互独立,且能列出独立方程的结点称为独立结点。
KVL独立方程

对于有n个结点,b条支路的连通图,有且仅有(b-n+1)个独立的KVL方程。将能列出独立KVL方程的回路称为独立回路。常用的独立回路:
- (b-n+1)个基本回路
- 平面电路的(b-n+1)个网孔
2b法/支路法
电路分析的任务,就是求出未知的支路电压和支路电流。标题所述的,就是求解电路最基本的两种方法。手工分析时,计算较为繁琐
2b法
以b个支路电压和b个支路电流为未知变量列写并求解方程的方法称为2b法。

下面以上图为例,说说列写步骤:
- 在a、b、c三个结点列写出(n-1)=3个独立KCL方程;选网孔列写出(b-n+1)=3个独立KVL方程。

- 根据元件的伏安关系,每条支路又能列写b=6个支路电压和电流方程。

- 解上述2b=12个独立方程,求出支路电流和电压。
支路法
以支路电流/电压为未知量列出方程,求解支路电流/电压,称为支路电流/电压法。
步骤如下:
- 选定各支路电流参考方向
- 对n-1个独立结点,列出独立KCL方程
- 选定b-n+1个独立回路(基本回路或网孔),指定回路绕行方向,根据KVL和OL列出回路电压方程。列写过程中,将支路电压用支路电流来表示
- 联立求解上述b个支路电流方程,求解题述的支路电压/功率
例1
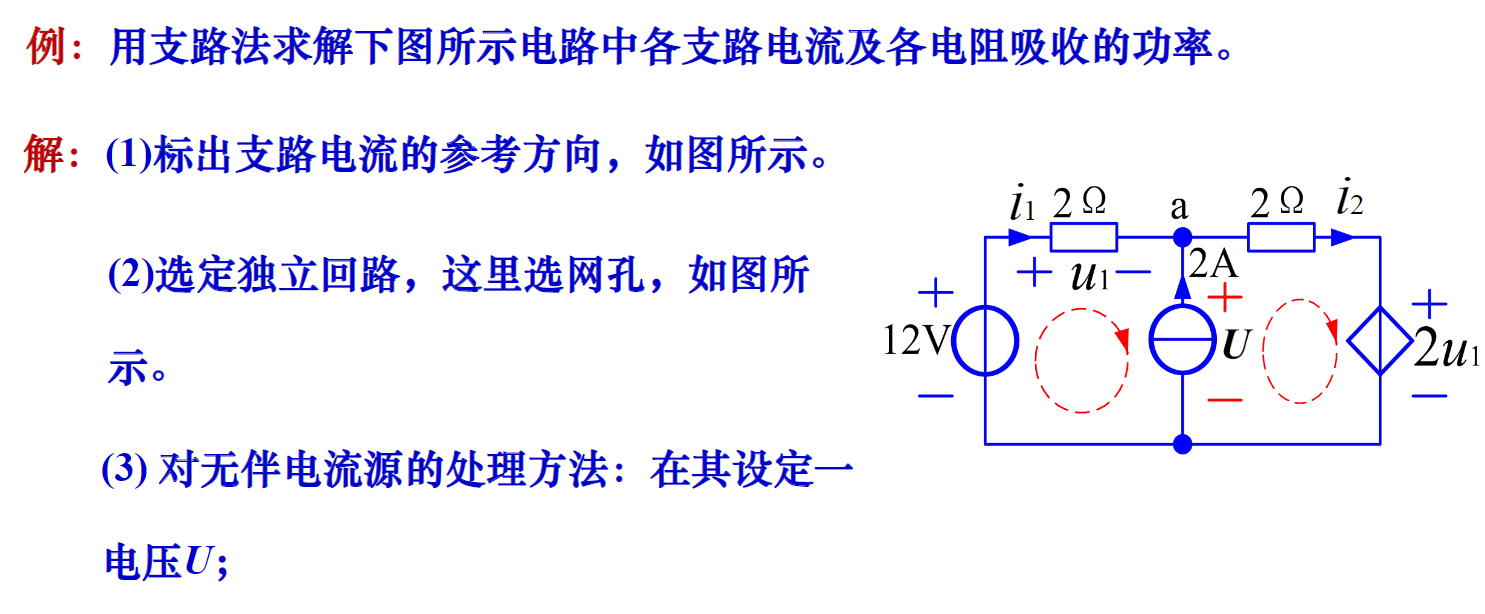
此处是重点!!!对于无伴电流源(也就是支路上只有一个电流源)的处理方法是,在其两端设定一个电压U,然后后续的回路法计算中,忽略它的电流。


回路法/网孔法
回路法,顾名思义,是以一组独立回路电流为变量并列出由前者表达的KVL方程的求解方法。通常选择基本回路为独立回路。这时,回路电流就是相对应的连枝电流。

对于上图(a),选定三个回路之后,对于节点123,根据KCL可得到各树枝电流为
$$
\left{
\begin{aligned}
i_4&=i_1-i_2\
i_5&=i_1+i_3\
i_6&=-i_2-i_3\
\end{aligned}
\right.
$$
将上式和上图对照,可得到树枝电流等于流经相关各回路电流的代数和。
随后,对于各回路应用KVL,并将其中的支电流改用回路电流表示,从而就得到了回路法的方程组。
戴维南等效电路
内容:一个线性含源网络N可以用一个电压源和一个电阻的组合等效代替。
其中,电压源记作$u_{oc}$,电阻记作$R_0$。
显然,使用该定理能够简化很多电路问题的求解。下面介绍戴维南等效电路的求法。
戴维南等效电阻的求解
大致有四个方法。不含受控源的有一种,含有受控源的有三种。
独立源置零法
将无受控源电路网N中的独立源置零,随后根据电路串并联关系和星角变换等方法求出从端口看进去的等效电阻$R_0$。
这里所说的独立源置零指的是:电压源替换为导线,电流源替换为开路。
外加电源法
令N中所有独立源置零,保留受控源,随后外加独立源。如果外加电流源,就以电压为响应;相反则以电流为响应。最后就能计算得出:
$$
R_0=\frac{u}{i}
$$
注意,对于电路网N而言,u和i是关联参考方向;但是对于外加的独立源而言,u和i是非关联参考方向。
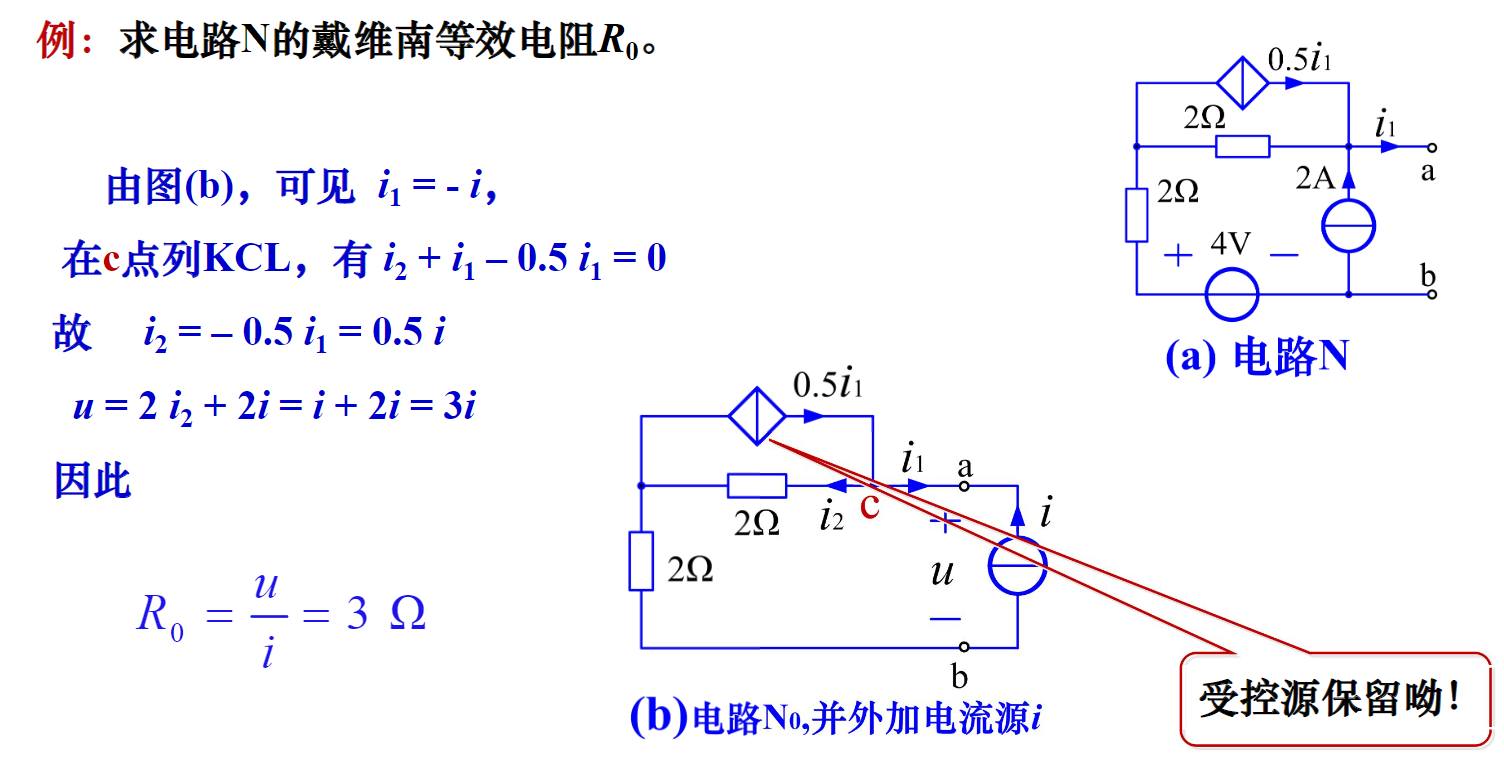
上面的例题中,i可以是给定的,也可以是变量。
开路短路法
计算电路的开路电压$u_{oc}$,短路电流$i_{sc}$,即可根据二者和$R_0$的关系求得$R_0$。
总结:
- 不含受控源的戴维南等效内阻的求解:独立源置零,运用电阻的串并联来求解其等效内阻
- 含受控源的戴维南等效电阻的求解:*外加电源法和开路短路法,以及端口的伏安关系法。*