第一章:电路的基本规律
本章主要关于电路的基本定理、基本器件以及电路的等效变换。
电路的等效
对于任何电路A,如果C和B接在A的端子上,电压、电流、功率完全一样,则称C与B等效。

- 例1:

“等效”是对于外电路而言的。因此,当外电路A发生变化时,C和B依旧等效才能称作等效。
- 例2:
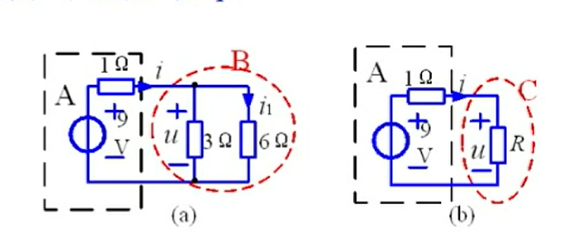
如图,将两个电阻替换成一个电阻,从而化简电路。
串并联等效
- 串联等效
特征:流过各电阻的电流是同一电流。


阻值和分压成正比
- 并联等效

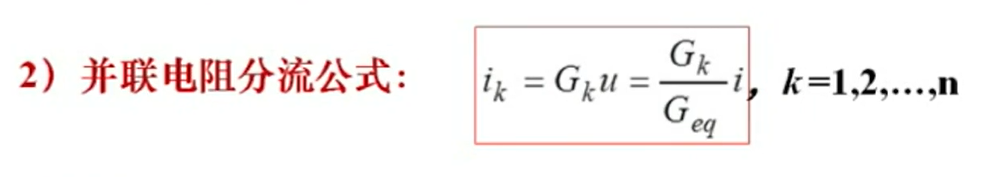
电导是电阻的倒数,即 $G = \frac{1}{R}$ ,单位是 $S$
- 混联等效
即:既有串联,又有并联
观察电路的结构特点和电压、电流关系
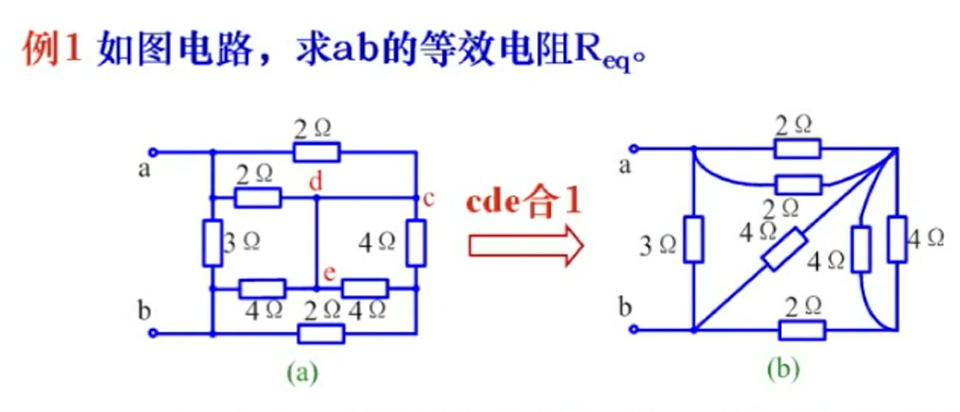
很快就能算出 $R_{eq}=1.5\Omega$
$\Delta$形Y形连接等效
- 问题的提出
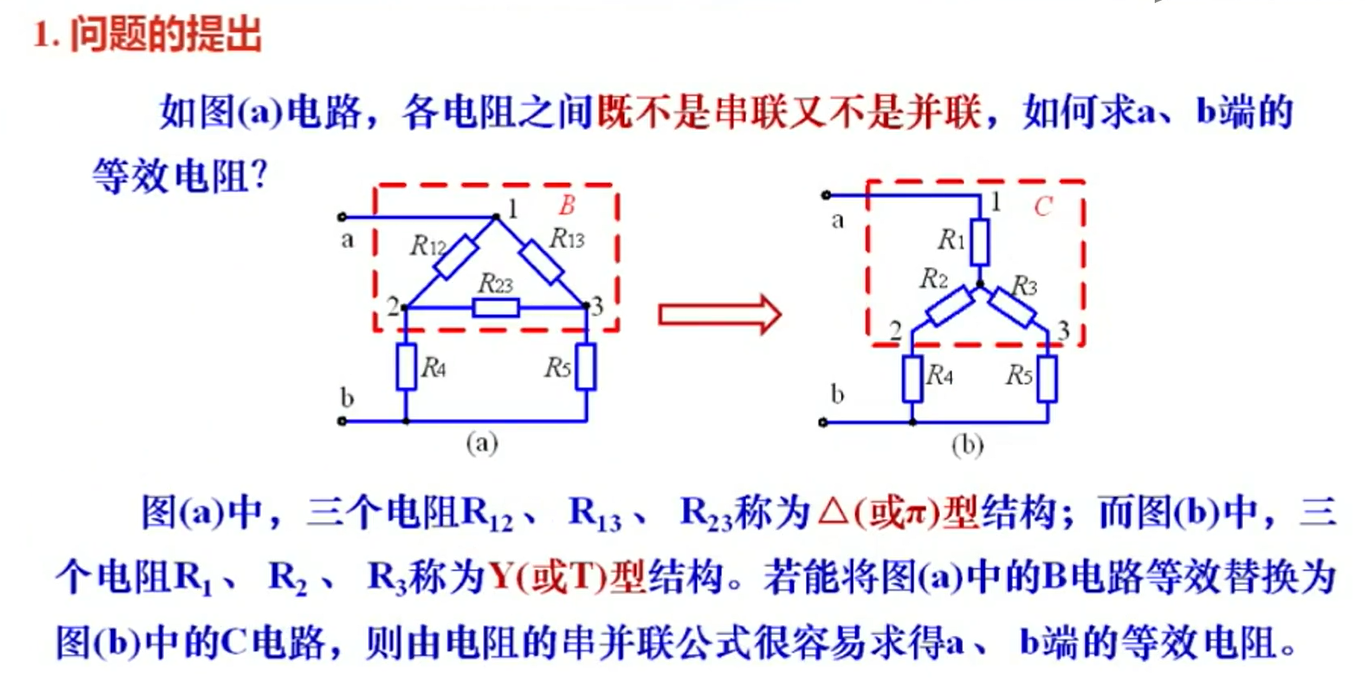
- 等效
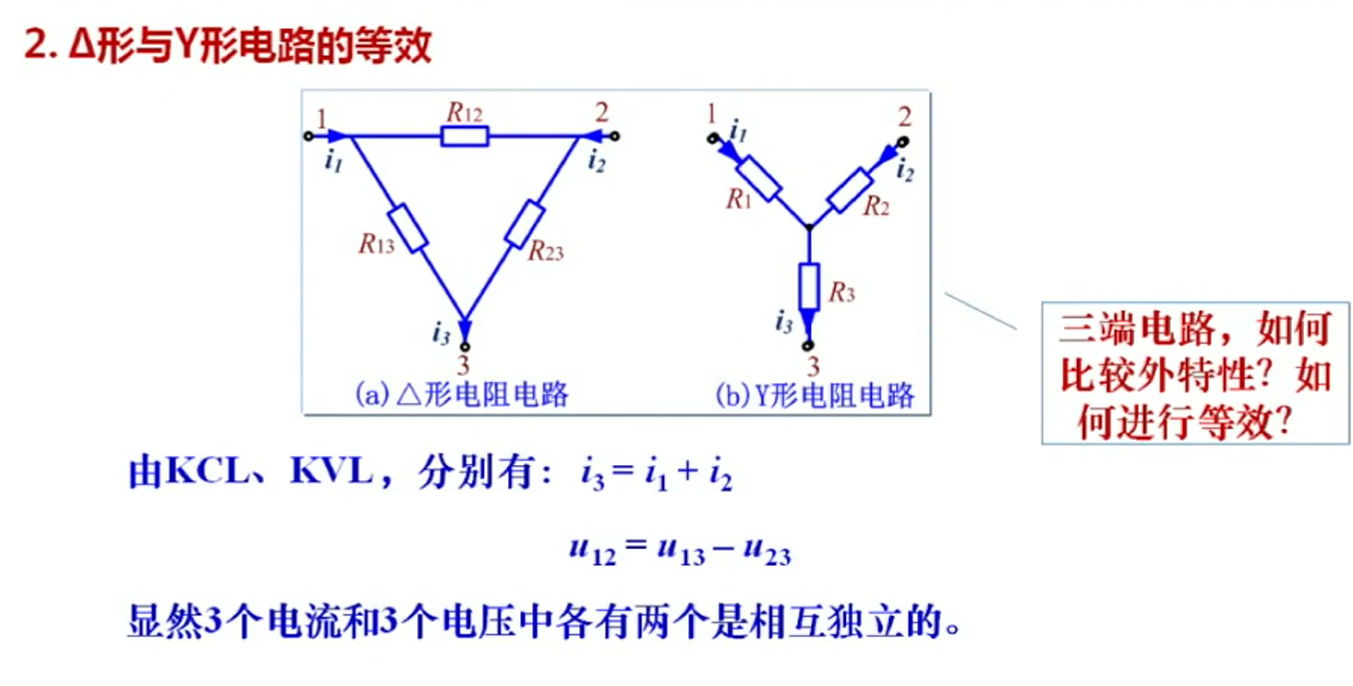
其中,2个支路的电流和电压独立。
对于图a中的三个支路,由KCL和OL得到关系:
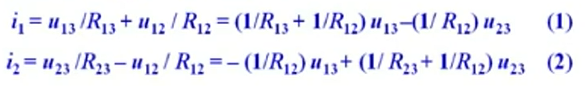
图b中,由KVL得:

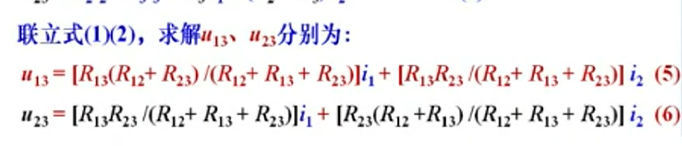
式3、5和式4、6应恒等。
结论:从 $\Delta$到Y:
$$
R_1=\frac{R_{12}R_{13}}{R_{12}+R_{13}+R_{23}}\
R_2=\frac{R_{12}R_{23}}{R_{12}+R_{13}+R_{23}}\
R_3=\frac{R_{13}R_{23}}{R_{12}+R_{13}+R_{23}}\
$$

从Y到 $\Delta$:
$$
R_{12}=\frac{R_1R_2+R_2R_3+R_3R_1}{R_3}\
R_{23}=\frac{R_1R_2+R_2R_3+R_3R_1}{R_1}\
R_{13}=\frac{R_1R_2+R_2R_3+R_3R_1}{R_2}\
$$

同时,若 $R_1=R_2=R_3=R_Y$,则 $R_{12}=R_{23}=R_{13}=R_\Delta$,且 $R_\Delta=3R_Y$
- 举例

这是一个桥接电路。
含受控源电阻的等效
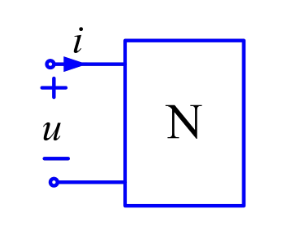
如图,u、i参考方向关联,因此定义其端口等效电阻为:
$$
R_{eq}=\frac{u}{i}
$$
$R_{eq}$的计算使用外加电流的方法:外加独立电流/电压源得到伏安关系,从而得到 $R_{eq}$。
- 例1
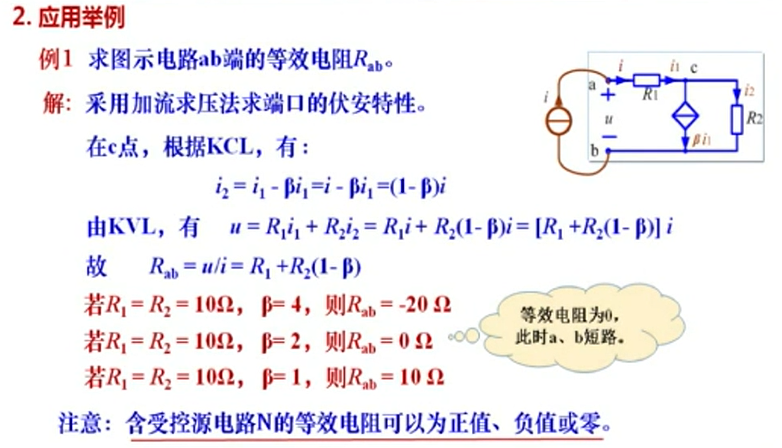
解题关键就是计算得到 $u$ 和 $i$,此时就可利用定义式得到等效电阻。
- 例2

独立源的串并联等效
- 电压源串联而成的二端电路,可以等效成一个电压源,其值为几个电压源的电压值代数和。
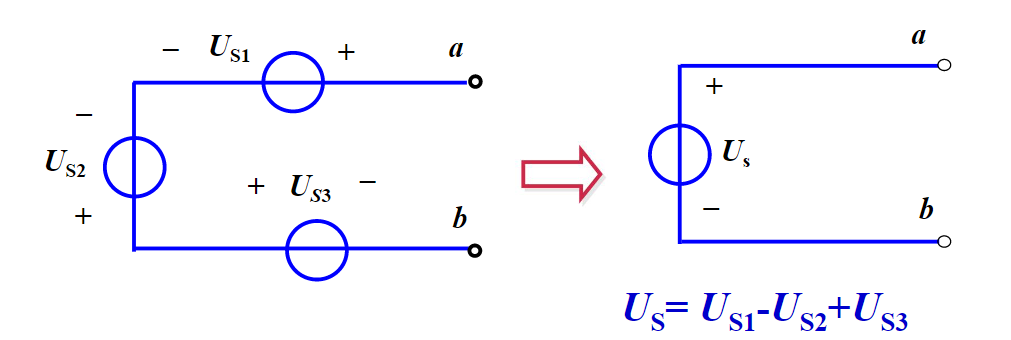
注意;方向一致、电压相等的电压源才能并联,否则违背KVL
- 多个电流源可以并联,等效为一个电流源,其值为各电流源 电流值的代数和。

同样地,电流值一致且方向相等的电流源才能串联,否则违背KCL
电流源与电压源/电阻串联:对外只等效为电流源。
电压源和电流源/电阻并联:对外只等效为电压源。

电源等效后的外特性不变。
实际电源的模型
将实际电源(例如干电池)外接滑动变阻器,得到其电源特性曲线:

令 $\frac{U_s}{I_s}=R_s$,得到解析式为:
$$
u=U_s-R_si
$$
这就是实际电源的电压源模型:电压源和内阻 $R_s$ 的串联。
若将表达式变形为关于 $i$ 的函数,则:
$$
i=I_s-\frac{u}{R_s}
$$
这就是实际电源的电流源模型:电流源和内阻 $R_s$ 的并联。
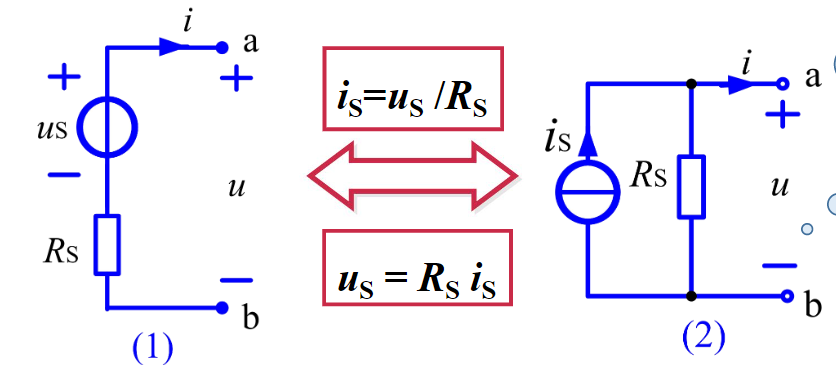
两模型的互换等效
由于前面两者的VCR(伏安关系)相同,所以实际电源的这两种模型电路是等效的。这也适用于受控电压/电流源,也就是说,受控源也可以等效互换。
互换时要注意电压源的电压极性与电流源电流的方向之间的关系。
- 例1
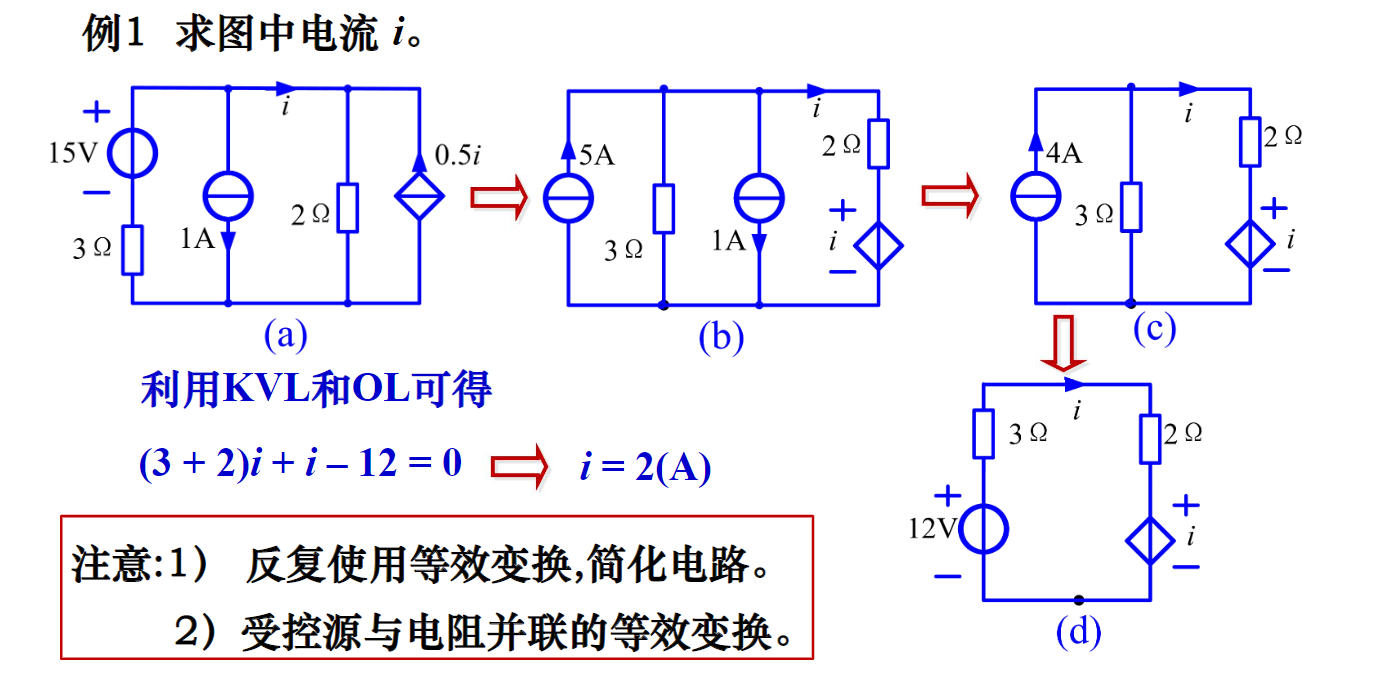
上面的例子通过源的等效变换和独立源的串并联等效,将电路化简为只含两个电源的电路,大大简化了电路。
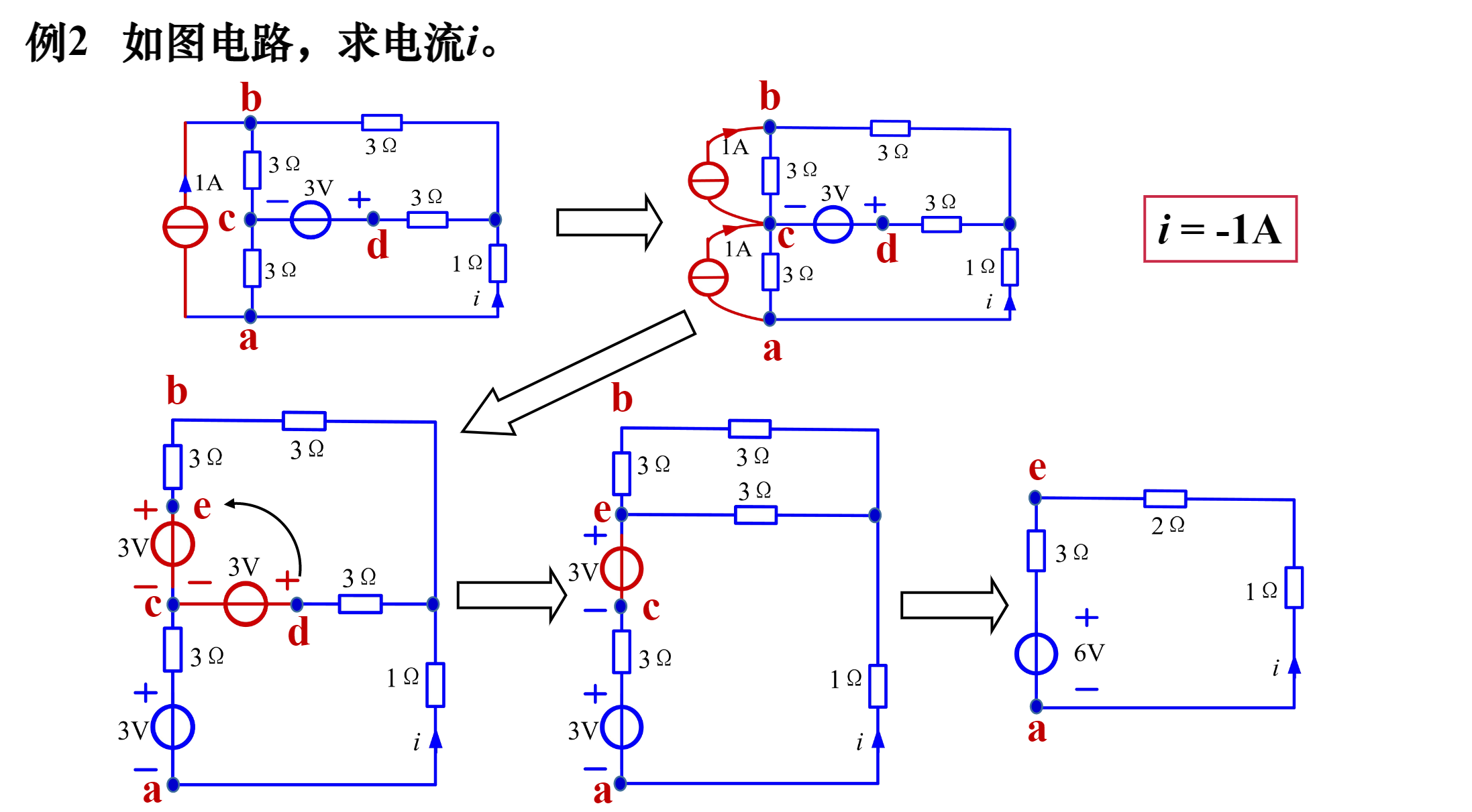
- 例2
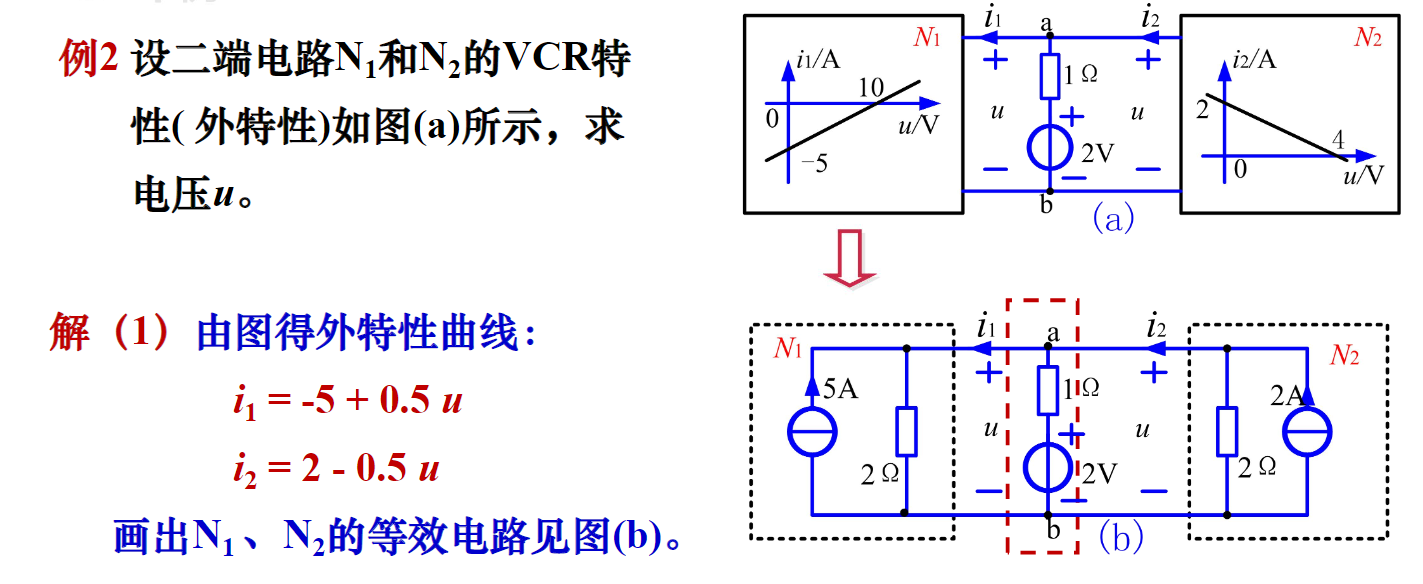
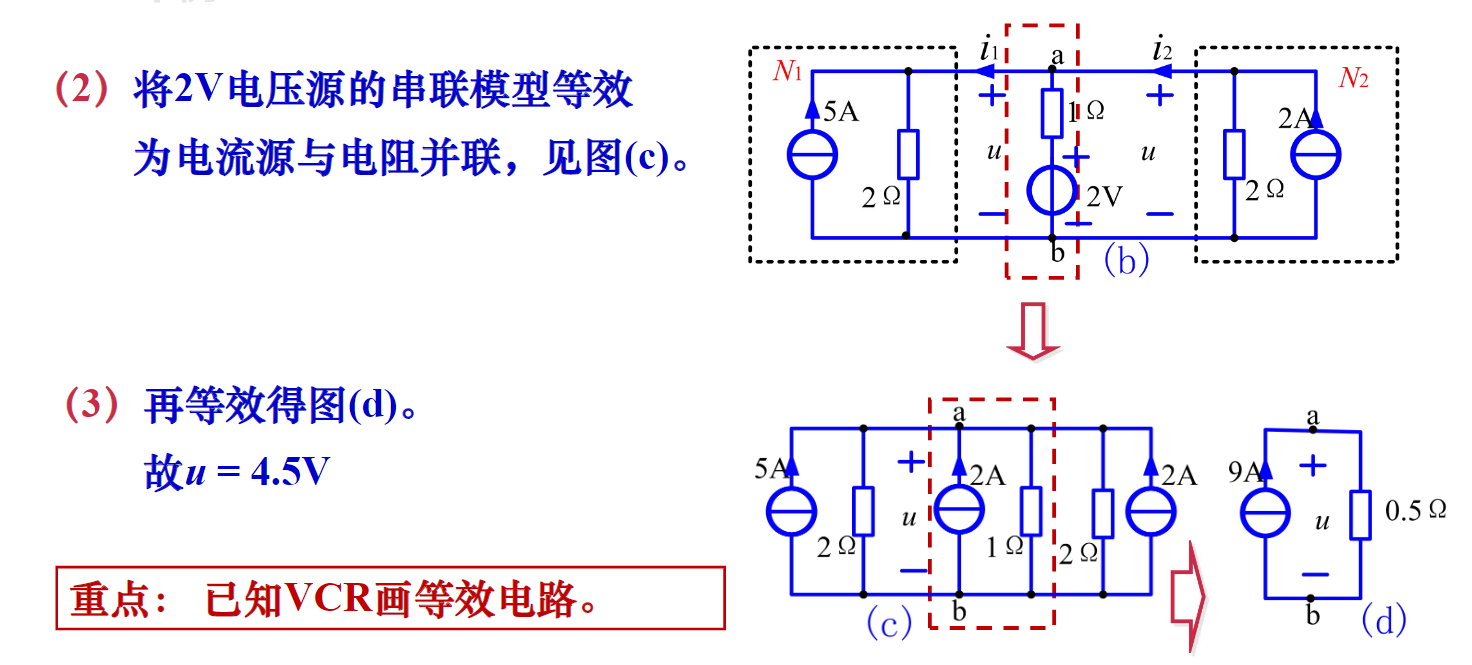
上面例题的关键是根据公式 $i=I_s-\frac{u}{R_s}$将实际电源变形为电流源。完成之后进行正常的电源等效合并简化电路即可。
总结
- 一个实际电路对应两个理想电源模型
- 实际电源的两种等效理想电源模型:
$$
i_S=\frac{u_S}{R_S} \
u_S=R_Si_S
$$ - 电路等效变换过程中,电路结构会发生变化,注意未知量是否变化
- 受控电压源/电流源+电阻也可以等效变换,不过注意变换过程中,控制两必须保留
电源的等效转移
电压源-等效变换
利用了bcde结点电位相等的特点,将电压源分拆到三路上。转移后的各回路的KVL方程应不变。

例如:
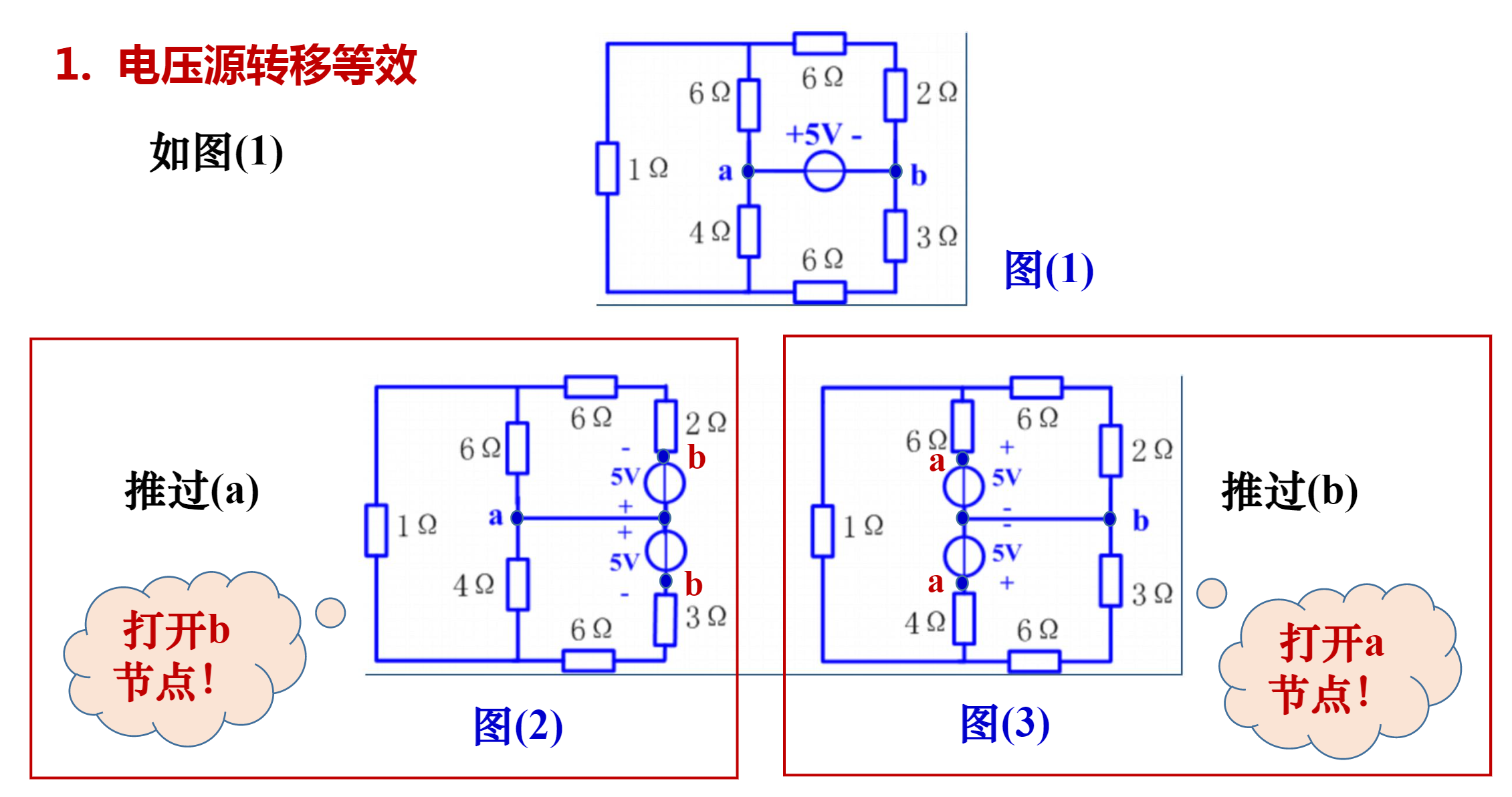
上图中有两种拆法,既可以拆到左边也可以拆到右边。
- 例1
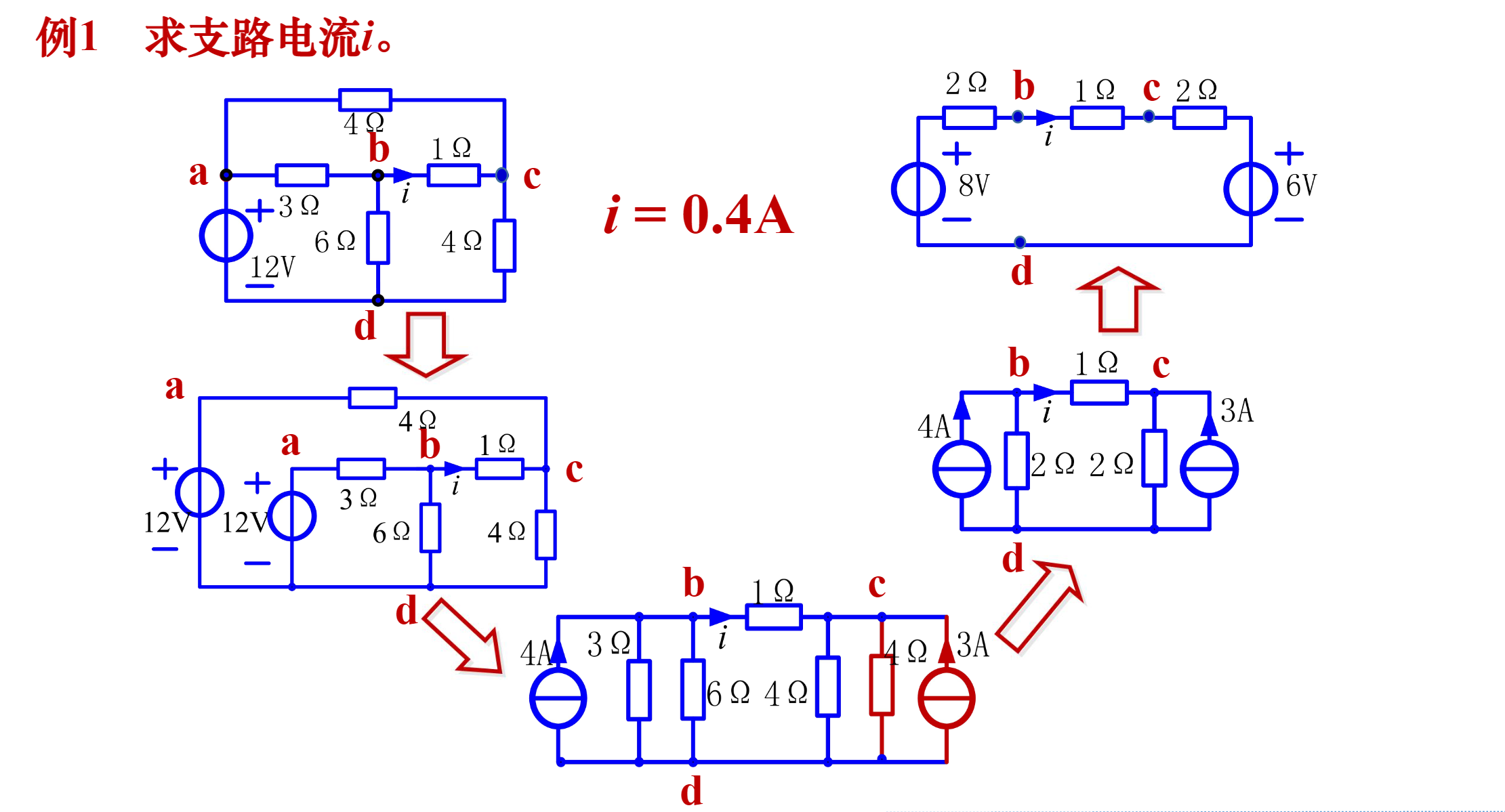
电流源-等效变换
从起点开始,选择一回路到终点,每条支路并联。转移后的KCL方程应保持不变。
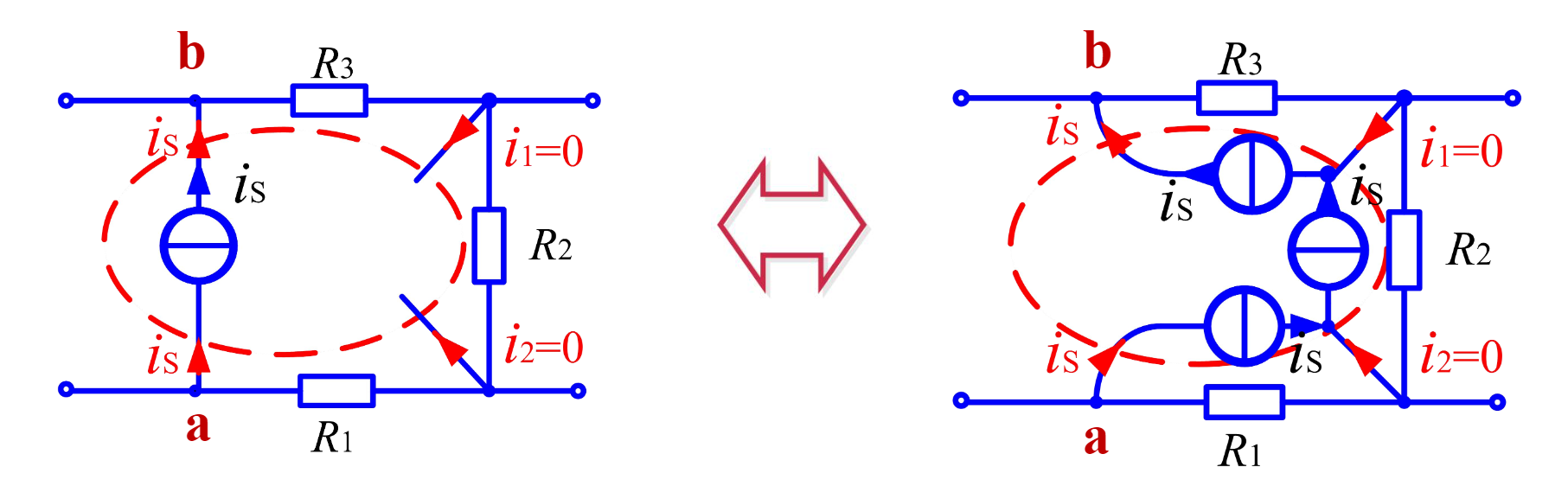
- 例2
电桥
顾名思义,“桥”是起连接作用的。电桥所连接的,则是电路。
将两个支路用电阻 $R_5$相连接,则 $R_1 \dots R_5$就形成了一个电桥。 $R_5$就是桥接电阻。
平衡电桥
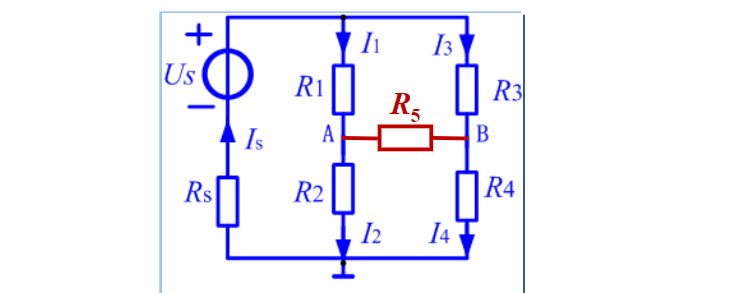
在上图中,如果存在:
$$
R_1R_4=R_2R_3
$$
则会有A,B两点等电位。这即是平衡电桥。
显然,平衡电桥具备下面的性质:
等电位点间连接任意电阻,都不影响外电路的支路量
也就是说,平衡电桥可以看作开路。
同时,将 $R_4$换为可调节电阻 $R$,电桥换为电流计 $A$,即可测量 $R_1$的阻值:
$$
R_x=\frac{R_2R_3}{R}
$$